Intervalos
Los intervalos matemáticos son una herramienta fundamental en las matemáticas, especialmente en el análisis y la teoría de conjuntos. Un intervalo es un conjunto de números reales que se encuentran dentro de un rango específico, definido por dos puntos extremos. Los intervalos se utilizan para describir y analizar conjuntos de números que satisfacen ciertas condiciones o propiedades.
¿Qué es un intervalo?
Son una herramienta fundamental para describir y analizar conjuntos de números reales, y tienen amplias aplicaciones en diversas áreas de las matemáticas y la ciencia.
Características
2. Inclusión: Un intervalo puede incluir o no sus puntos extremos.
3. Longitud: La longitud de un intervalo es la diferencia entre sus puntos extremos (b - a).
4. Dirección: Un intervalo puede ser abierto, cerrado, semiabierto o infinito.
Elementos de los intervalos:
2. Límite superior (b): El punto más grande del intervalo.
3. Puntos intermedios: Los números reales que se encuentran dentro del intervalo, excluyendo los puntos extremos.
4. Extremos: Los puntos que definen el intervalo (a y b).
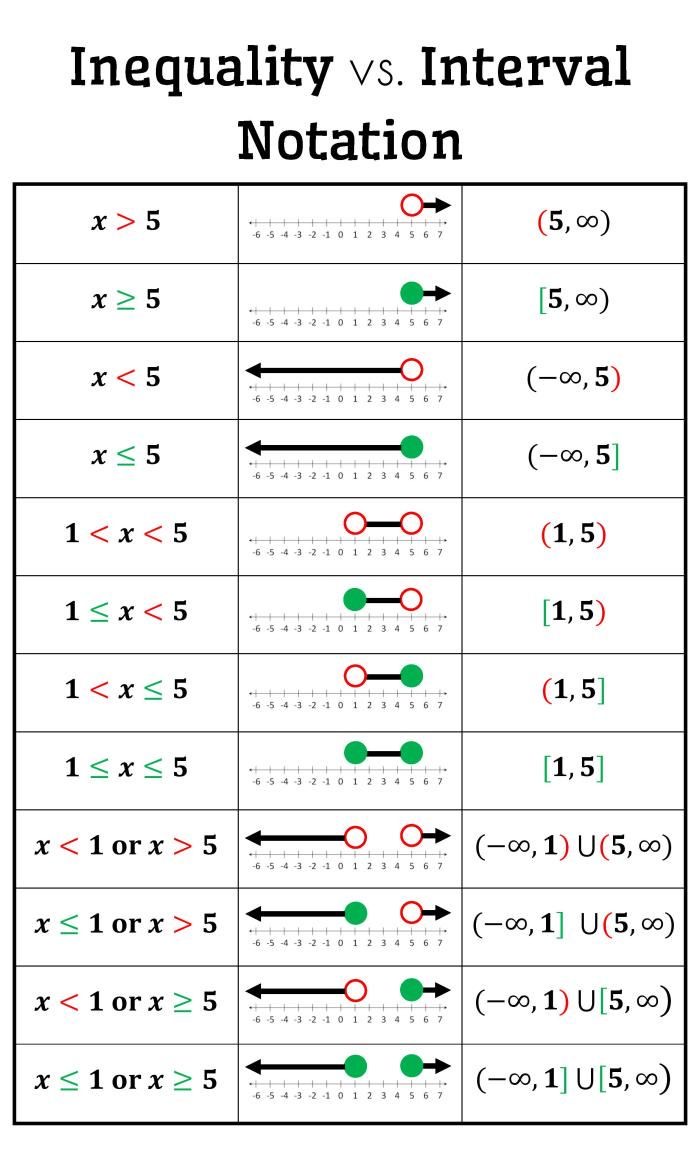
Tipos de intervalos
2. Intervalo cerrado: [a, b] = { x | a ≤ x ≤ b }
3. Intervalo semiabierto: (a, b] = { x | a < x ≤ b } o [a, b) = { x | a ≤ x < b }
4. Intervalo infinito: (-∞, a) = { x | x < a } o (a, ∞) = { x | x > a }
Propiedades de los intervalos:
2. Intersección: La intersección de dos intervalos es otro intervalo.
3. Unión: La unión de dos intervalos es otro intervalo.
4. Complemento: El complemento de un intervalo es el conjunto de números reales que no están en el intervalo.
Aplicaciones de los intervalos
2. Teoría de conjuntos: Estudio de conjuntos y relaciones.
3. Geometría: Estudio de figuras y espacios.
4. Estadística: Estudio de datos y probabilidad.
Graficación de Intervalos
*Graficación de Intervalos en la Recta Numérica*
1. Dibuja una recta numérica horizontal.
2. Selecciona un punto inicial (a) y un punto final (b) en la recta numérica.
3. Utiliza los siguientes símbolos para representar los intervalos:
- Paréntesis abierto ( para indicar que el punto inicial no está incluido.
- Corchete [ para indicar que el punto inicial está incluido.
- Paréntesis cerrado ) para indicar que el punto final no está incluido.
- Corchete ] para indicar que el punto final está incluido.
*Ejemplos de Graficación de Intervalos*
1. Intervalo abierto (a, b):
[a------b)
2. Intervalo cerrado [a, b]:
[a------b]
3. Intervalo semiabierto [a, b):
[a------b)
4. Intervalo semiabierto (a, b]:
(a------b]
*Colores y Símbolos Utilizados*
- Punto inicial (a): círculo abierto o cerrado.
- Punto final (b): círculo abierto o cerrado.
- Intervalo: línea continua o discontinua.
- Puntos excluidos: círculo abierto con una cruz.
*Herramientas para Graficar Intervalos*
1. Papel y lápiz.
2. Software de graficación (GeoGebra, Desmos, etc.).
3. Calculadoras gráficas.
Recuerda que la graficación de intervalos es una herramienta visual para representar conjuntos de números y facilitar la comprensión de conceptos matemáticos.
Video para la graficación de intervalos
Juego didáctico para reforzar los conocimientos
Ejercicios de los intervalos
Consejos para realizar los intervalos
1. Asegúrate de entender el concepto de intervalo y sus propiedades.
2. Utiliza la notación correcta para representar intervalos (paréntesis, corchetes, etc.).
3. Verifica que los puntos extremos estén correctamente definidos.
Consejos para Graficar Intervalos:
1. Utiliza una recta numérica horizontal para graficar intervalos.
2. Asegúrate de incluir los puntos extremos correctos (abierto o cerrado).
3. Utiliza colores y símbolos para destacar los puntos excluidos.
Consejos para Resolver Problemas de Intervalos:
1. Lee cuidadosamente el enunciado del problema.
2. Identifica los puntos extremos y el tipo de intervalo.
3. Utiliza las propiedades de los intervalos para resolver el problema.
Consejos para Trabajos y Exámenes
1. Revisa los conceptos básicos de intervalos antes de realizar un trabajo o examen.
2. Asegúrate de entender las aplicaciones de los intervalos en diferentes áreas de la matemática.
3. Practica resolver problemas de intervalos para mejorar tu comprensión y habilidades.
Recursos Adicionales:
1. Utiliza software de graficación como GeoGebra o Desmos.
2. Consulta libros de texto y recursos en línea.
3. Busca tutoriales y videos explicativos en YouTube.
Errores Comunes a Evitar
1. Confundir los puntos extremos.
2. No incluir los puntos extremos correctos.
3. No utilizar la notación correcta.