Funciones y relación
Funciones
Las funciones y relaciones son conceptos fundamentales en las matemáticas que permiten describir y analizar la conexión entre variables y conjuntos de números. Estos conceptos son esenciales en diversas áreas de la matemática, como el álgebra, el cálculo, la geometría y la estadística.
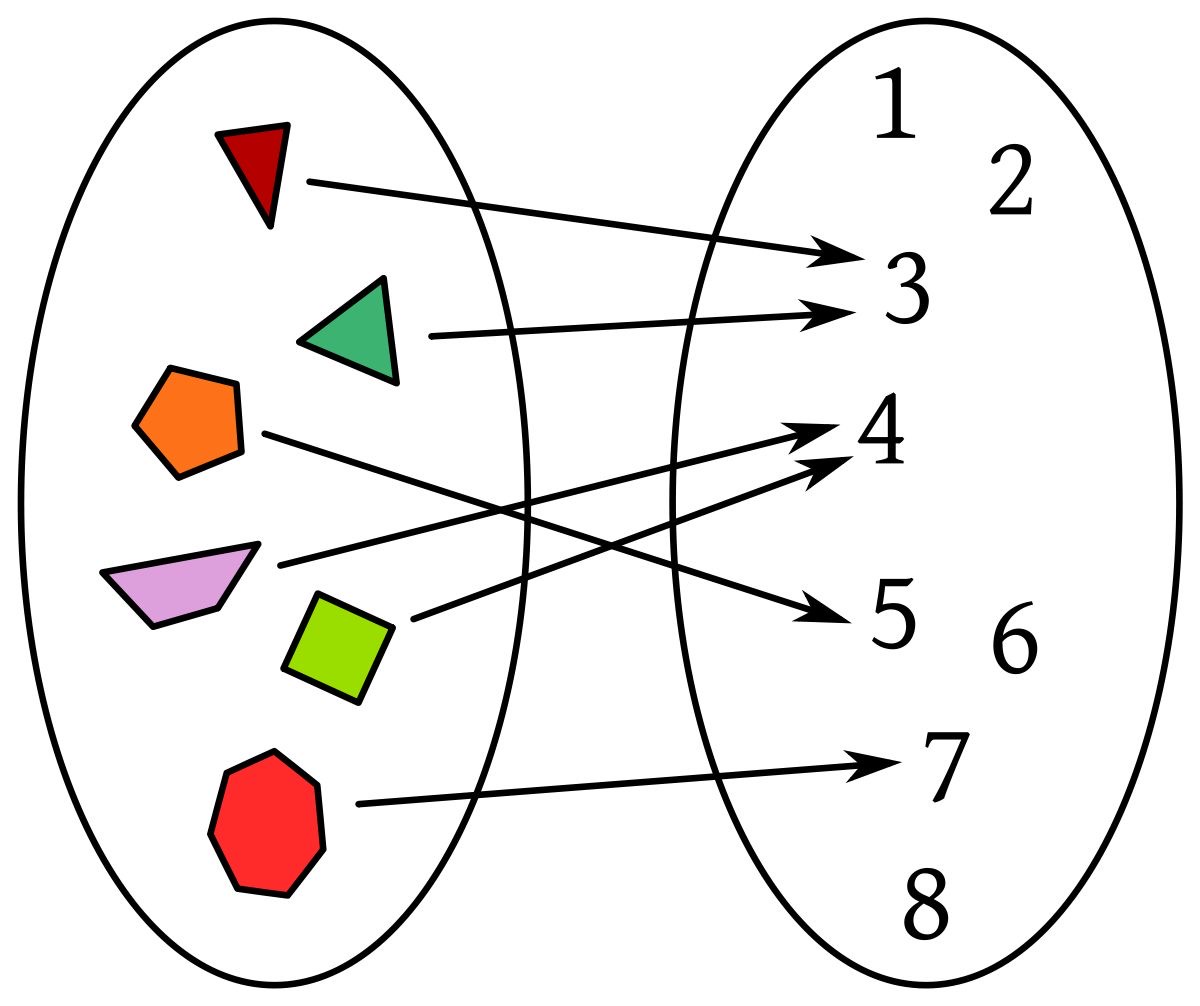
¿Qué es una función?
Características de las funciones
2.Rango: Conjunto de valores de salida.
3. Unicidad: Cada valor de entrada corresponde a un único valor de salida.
4. Dirección: Las funciones pueden ser crecientes, decrecientes o constantes.
Tipos de funciones:
2. Función cuadrática: f(x) = ax^2 + bx + c
3. Función polinómica: f(x) = a_nx^n + a_{n-1}x^{n-1} + ... + a_1x + a_0
4. Función trigonométrica: f(x) = sen(x), cos(x), tan(x), etc.
5. Función exponencial: f(x) = a^x
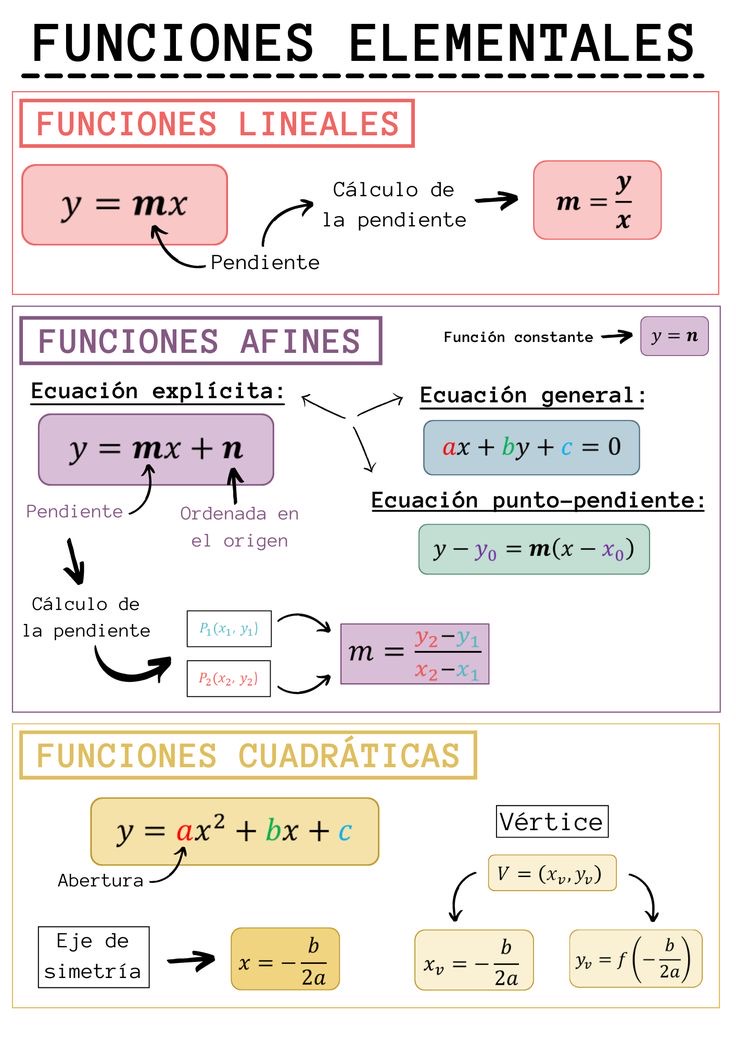
Para definir la función
2. Define la regla de correspondencia entre el dominio y el rango.
3. Utiliza notación matemática para representar la función, por ejemplo: f(x) = ...
Propiedades de las funciones
2. Inyectividad y sobreyectividad
3. Composición de funciones
4. Inversa de una función
5. Simetría y reflexividad
Video a cerca del dominio y rango
Herramienta para crear funciones
2. Software de matemáticas (GeoGebra, Desmos, etc.)
3. Papel y lápiz
4. Tablas de valores
Graficas de funciones
2. Identifica los puntos clave de la función, como interceptos y vértices.
3. Analiza la forma y el comportamiento de la función.
Video para aprender a graficar
Ejemplos de Funciones
2. f(x) = x^2 - 4
3. f(x) = 3sen(x)
4. f(x) = 2^x
Aplicaciones de las funciones
1. Modelización de fenómenos físicos.
2. Análisis de datos.3. Resolución de ecuaciones.
4. Optimización.
5. Simulación.

Funciones inyectivas, sobreyectivas y biyectivas
Una función f es inyectiva si:
1. Cada valor de salida corresponde a un único valor de entrada.
2. No hay dos valores de entrada diferentes que produzcan el mismo valor de salida.
Ejemplo: f(x) = 2x
*Propiedades:
1. Si f(a) = f(b), entonces a = b.
2. La función es creciente o decreciente.
-Función Sobreyectiva (Onto)
Una función f es sobreyectiva si:
1. Todos los valores de salida están cubiertos.
2. Cada valor de salida corresponde a al menos un valor de entrada.
Ejemplo: f(x) = x^2
*Propiedades:
1. La función tiene un rango igual al conjunto de salida.
2. La función puede tener valores de entrada repetidos.
-Función Biyectiva (Uno a Uno y Onto)
Una función f es biyectiva si:
1. Es inyectiva y sobreyectiva.
2. Cada valor de salida corresponde a un único valor de entrada y todos los valores de salida están cubiertos.
Ejemplo: f(x) = x
*Propiedades:
1. La función es creciente o decreciente.
2. La función tiene un rango igual al conjunto de salida.
3. La función tiene una inversa.
*Resumen:
- Inyectiva: Uno a uno (cada salida corresponde a un único entrada).
- Sobreyectiva: Onto (todos los valores de salida están cubiertos).
- Biyectiva: Uno a uno y onto (combinación de inyectiva y sobreyectiva).
Video para implementar información
Juegos didacticos de las funciones
Ejercicios para las funciones
Consejos para realizar funciones
1. Define claramente el dominio y rango de la función.
2. Utiliza notación matemática estándar.
3. Verifica la consistencia de la función.
4. Utiliza gráficas para visualizar la función.
-Consejos para Definir la Función:
1. Identifica el tipo de función (lineal, cuadrática, polinómica, etc.).
2. Define la fórmula de la función.
3. Verifica que la función sea bien definida.
-Consejos para Trabajar con Funciones:
1. Utiliza las propiedades de las funciones (como la linealidad o la simetría).
2. Utiliza técnicas de cálculo (como la derivada o la integral).
3. Utiliza herramientas gráficas para visualizar la función.
-Consejos para Resolver Problemas:
1. Lee cuidadosamente el enunciado del problema.
2. Identifica los datos y las incógnitas.
3. Utiliza técnicas de resolución de ecuaciones.
4. Verifica la solución.
-Herramientas Útiles:
1. Calculadoras gráficas.
2. Software de matemáticas (como GeoGebra o Desmos).
3. Tablas de valores.
4. Gráficas.
-Errores Comunes a Evitar:
1. No verificar la consistencia de la función.
2. No definir claramente el dominio y rango.
3. No utilizar notación matemática estándar.
4. No verificar la solución.
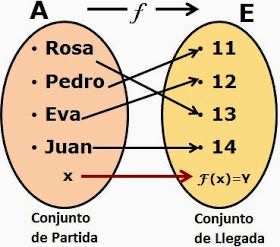
Relaciones
¿Qué es una relación?
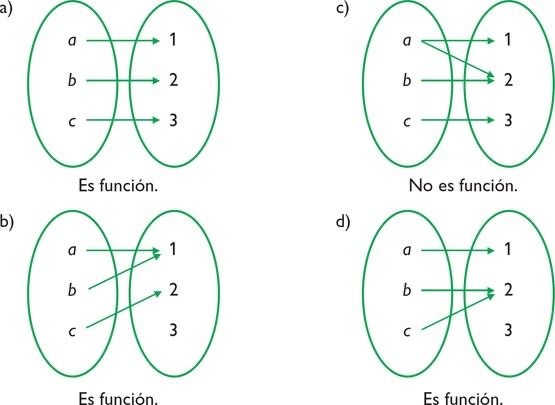
Características de las Relaciones
1. Reflexividad: (a, a) ∈ R para todo a ∈ A.
2. Simetría: si (a, b) ∈ R, entonces (b, a) ∈ R.
3. Transitividad: si (a, b) ∈ R y (b, c) ∈ R, entonces (a, c) ∈ R.
4. Antisimetría: si (a, b) ∈ R y (b, a) ∈ R, entonces a = b.
Características Específicas:
1. Relación de Igualdad: R es una relación de igualdad si (a, b) ∈ R implica a = b.
2. Relación de Orden: R es una relación de orden si (a, b) ∈ R implica a ≤ b.
3. Relación de Equivalencia: R es una relación de equivalencia si es reflexiva, simétrica y transitiva.
4. Relación de Función: R es una relación de función si cada elemento de A se relaciona con un único elemento de B.
Propiedades de las Relaciones
2. Estabilidad: la relación se mantiene bajo pequeñas variaciones.
3. Monotonía: la relación se mantiene bajo ciertas condiciones de orden.
Tipos de relaciones
2. Relación Sobre (Sobreyectiva).
3. Relación Biunívoca (Biyectiva).
4. Relación de Equivalencia.
Video para implementar información
Importancia de las Relaciones
2. *Análisis*: las relaciones permiten analizar y entender la estructura de los conjuntos.
3. *Generalización*: las relaciones permiten generalizar resultados a diferentes contextos.
Aplicaciones de las Relaciones
1. Teoría de Conjuntos: relaciones entre conjuntos.
2. Álgebra: relaciones entre elementos de un grupo o anillo.
3. Geometría: relaciones entre puntos y rectas.
4. Análisis: relaciones entre funciones y límites.
5. Ciencia de la Computación: relaciones entre algoritmos y datos.
Juegos didácticos de las Relaciones
Ejercicios:
Consejos para las Relaciones
1. Define claramente los conjuntos involucrados.
2. Establece la relación entre los elementos de los conjuntos.
3. Verifica que la relación sea bien definida.
4. Utiliza notación matemática adecuada.
-Consejos para Definir la Relación:
1. Identifica el tipo de relación (igualdad, orden, equivalencia, función).
2. Establece las condiciones para que la relación sea verdadera.
3. Utiliza propiedades matemáticas (reflexividad, simetría, transitividad).
-Consejos para Verificar la Relación:
1. Verifica que la relación sea reflexiva, simétrica y transitiva (si corresponde).
2. Comprueba que la relación sea consistente con las condiciones establecidas.
3. Utiliza ejemplos para verificar la relación.
-Consejos para Representar la Relación:
1. Utiliza diagramas de Venn o gráficos para representar la relación.
2. Utiliza notación matemática adecuada (por ejemplo, ∈, ⊆, =).
3. Utiliza tablas o matrices para representar la relación.
-Consejos para Aplicar la Relación:
1. Identifica las aplicaciones de la relación en diferentes áreas de la matemática.
2. Utiliza la relación para resolver problemas.
3. Verifica que la relación sea válida en diferentes contextos.
-Errores Comunes a Evitar:
1. No definir claramente los conjuntos involucrados.
2. No verificar que la relación sea bien definida.
3. No utilizar notación matemática adecuada.
-Recursos Adicionales:
1. Libros de texto de matemáticas.
2. Recursos en línea (Khan Academy, Mathway, etc.).
3. Software de matemáticas (GeoGebra, Desmos, etc.).