Parábolas
Este apartado sirve para entender a grandes rasgos la parábola dando la información de: Qué es, características, en qué se relaciona su vida diaria, tipos de parábolas, fórmulas, tutoriales, ejercicios y consejos.
¿Qué es una parábola?
Una parábola es una curva geométrica que se utiliza para modelar fenómenos físicos y matemáticos.
La parábola es una herramienta fundamental en matemáticas y física para modelar y analizar fenómenos complejos.
La fórmula de una parábola puede variar dependiendo de su orientación y posición en el plano cartesiano.
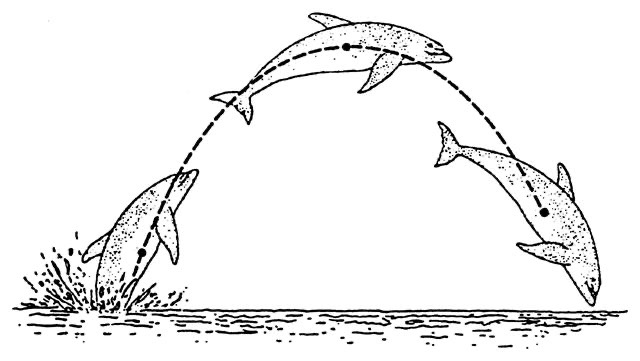
Características de la parábola:
- Forma de U que se abre hacia arriba o hacia abajo
- Puede tener un vértice (punto más alto o más bajo)
- Puede tener una dirección horizontal o vertical
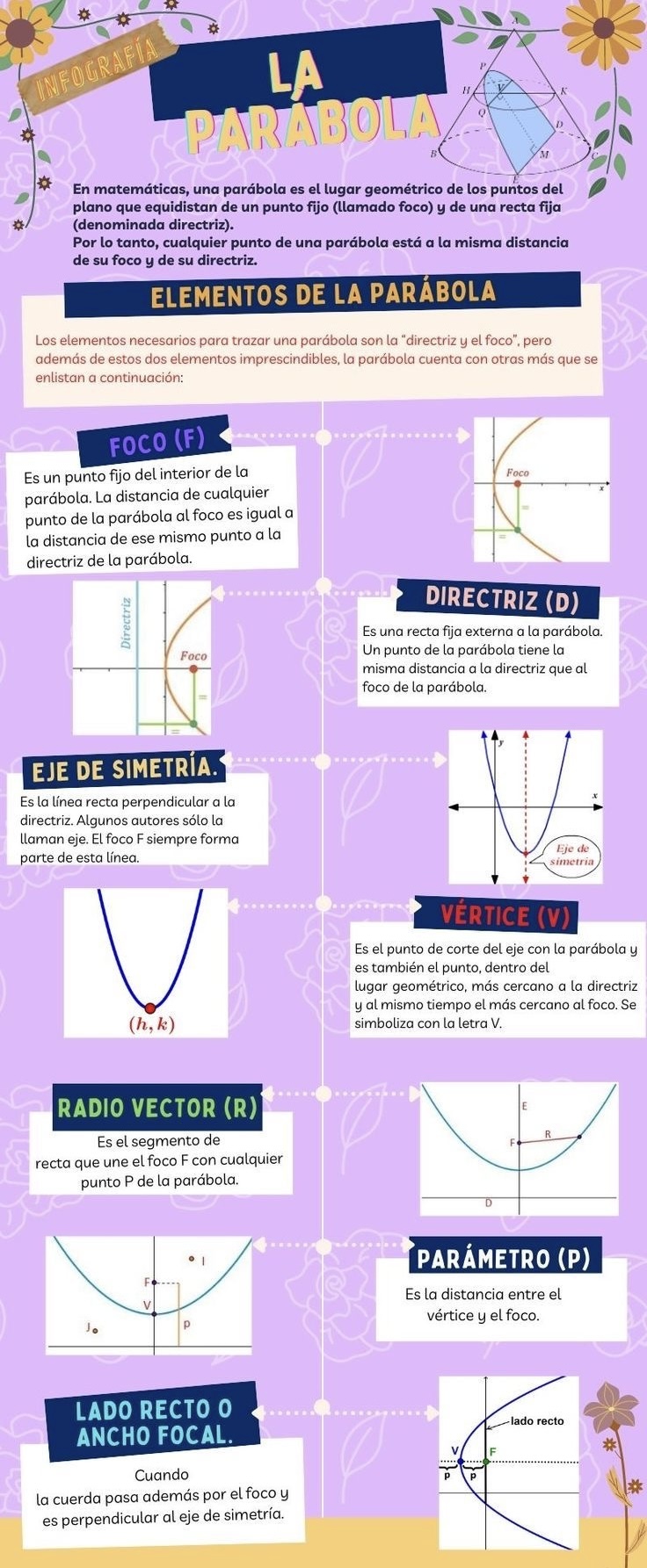
Elementos de la Parábola:
- Es el punto más alto o más bajo de la parábola.- Es el centro de simetría de la parábola.- Se denota como (h, k).
2. Foco (F)*
- Es un punto que se encuentra en el eje de simetría de la parábola.- Es el punto desde el cual se mide la distancia focal.- Se denota como (h, k + p) para parábolas verticales o (h + p, k) para parábolas horizontales.
3. Directriz (D)*
- Es una recta que se encuentra a una distancia p del vértice.- Es perpendicular al eje de simetría de la parábola.- Se denota como y = k - p para parábolas verticales o x = h - p para parábolas horizontales.
4. Eje de Simetría*
- Es la recta que pasa por el vértice y el foco.- Es perpendicular a la directriz.- Se denota como x = h para parábolas verticales o y = k para parábolas horizontales.
5. Distancia Focal (p)*
- Es la distancia entre el vértice y el foco.- Es igual a 1/4a, donde a es el coeficiente que determina la curvatura de la parábola.
6. Coeficiente de Curvatura (a)*
- Determina la forma y la curvatura de la parábola.- Un valor positivo de a indica una parábola que se abre hacia arriba.- Un valor negativo de a indica una parábola que se abre hacia abajo.
7. Punto de Intersección*
- Es el punto donde la parábola intersecta con el eje x o el eje y.
8. Brazos de la Parábola*
- Son las dos partes de la parábola que se extienden desde el vértice hacia arriba o hacia abajo.
Estos son los elementos básicos de una parábola. Espero que esta información te sea útil.
Video para entender los conceptos principales:
Ejemplos de Parábola en la vida diaria:
- La trayectoria de un objeto lanzado al aire (parábola vertical)
- El reflejo de una luz en un espejo parabólico (parábola horizontal)
- La forma de un arco de puente (parábola invertida)
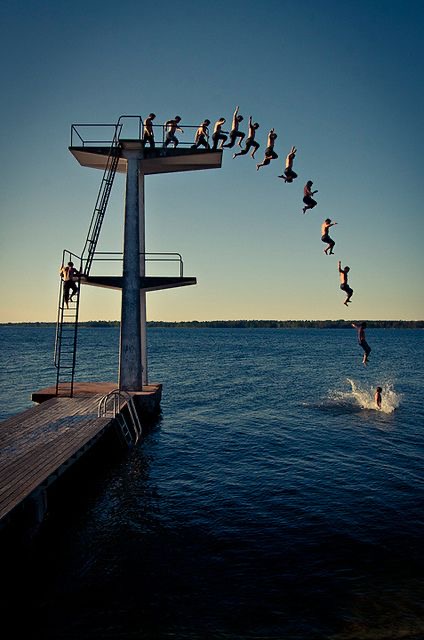
Tipos de Parábolas:
*Parábola vertical (y = ax^2 + bx + c)
Elementos de la Parábola vertical:
- a es el coeficiente que determina la curvatura de la parábola
- b es el coeficiente que determina la posición horizontal de la parábola
- c es el coeficiente que determina la posición vertical de la parábola.
Elementos de la Parábola horizontal:
- a es el coeficiente que determina la curvatura de la parábola
- b es el coeficiente que determina la posición vertical de la parábola
- c es el coeficiente que determina la posición horizontal de la parábola.
*Parábola oblicua (combinación de vertical y horizontal). La fórmula general de una parábola en forma de vértice es:
y = a(x - h)^2 + k
Elementos de la parábola oblicua:
- (h, k) es el vértice de la parábola
- a es el coeficiente que determina la curvatura de la parábola
* Parábola en Forma de Intersección. La fórmula general de una parábola en forma de intersección es:
y = ax^2 + bx + c
Elementos de la Parábola en forma de intersección:
- x = -b / 2a es la coordenada x del vértice
- y = c - b^2 / 4a es la coordenada y del vértice
Tutoriales para complementar información
Parábola con el vértice fuera del origen:
y = a(x - h)^2 + k
donde:
- (h, k) es el vértice de la parábola
- a es el coeficiente que determina la curvatura de la parábola
Esta fórmula se puede expandir para obtener:
y = a(x^2 - 2hx + h^2) + k
y = ax^2 - 2ahx + ah^2 + k
Comparando esta fórmula con la fórmula estándar de una parábola:
y = ax^2 + bx + c
se puede ver que:
- b = -2ah
- c = ah^2 + k
Ejemplo:
y = (x - 2)^2 + 3
En este ejemplo:
- h = 2
- k = 3
- a = 1
La parábola tiene su vértice en (2, 3) y se abre hacia arriba.
Otro ejemplo:
y = -(x + 1)^2 + 2
En este ejemplo:
- h = -1
- k = 2
- a = -1
La parábola tiene su vértice en (-1, 2) y se abre hacia abajo.
Para graficar una parábola con el vértice fuera del origen, se pueden seguir los siguientes pasos:
1. Identificar el vértice (h, k)
2. Identificar el coeficiente de curvatura (a)
3. Graficar la parábola utilizando la fórmula y = a(x - h)^2 + k
Video para implementar la información:
Juegos didácticos sobre las parabolas:
Ejercicios para descargar sobre las parábolas:
Consejos para realizar las parábolas:
2. Identifica el tipo de parábola (vertical u horizontal) y ajusta la fórmula según sea necesario.
3. Verifica que los coeficientes de la fórmula estén correctamente ordenados.
1. Identifica el vértice y marca su posición en el gráfico.
2. Determina la dirección de la parábola (hacia arriba o hacia abajo) según el signo del coeficiente de curvatura.
3. Marca la directriz y el foco para ayudarte a graficar la parábola.
4. Utiliza una cuadrícula para ayudarte a graficar la parábola con precisión.
*Consejos para resolver problemas de parábolas:1. Lee cuidadosamente el problema y identifica los datos proporcionados.
2. Determina qué tipo de problema es (encontrar el vértice, la directriz, el foco, etc.).
3. Utiliza la fórmula de la parábola para resolver el problema.
4. Verifica tus resultados para asegurarte de que sean precisos.
*Consejos para evitar errores comunes:1. Asegúrate de no confundir los coeficientes de la fórmula.
2. No olvides incluir el signo del coeficiente de curvatura.
3. Verifica que la parábola esté graficada en la dirección correcta.
4. No te olvides de marcar la directriz y el foco.